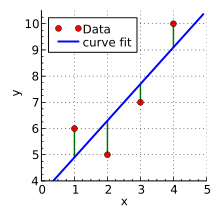
逻辑回归与线性回归是什么关系呢?
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model)。
逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。
因此与线性回归有很多相同之处,去除Sigmoid映射函数的话,逻辑回归算法就是一个线性回归。可以说,逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
什么是回归?
分类和回归是两类监督式机器学习算法问题。监督式机器学习使用算法来训练模型,以在包含标签和特征的数据集中找规律。
分类根据已知物品的已标记示例来预测一个物品属于哪个类别。
回归可估算目标结果标签与一个或多个特征变量之间的关系,以预测连续数值。许多监督式学习算法(例如决策树)可用于分类或回归。
统计回归分析从数学角度确定因变量与一个或多个自变量之间的关系。回归算法类型众多。
线性回归是一种用于回归的算法,以预测数值,例如房价。
逻辑回归是一种用于分类的算法,以预测物品属于某个类别的概率,例如电子邮件为垃圾邮件的概率。
什么是线性回归?
线性回归可通过一组数据点来拟合线性模型,以便估算目标结果标签与一个或多个特征变量之间的关系,从而预测数值。输出值 y(标签)可预测为一条直线,且该直线可用如下表达式表示:
y = 截距 + ci * xi + 误差
其中 xi 为输入变量(特征),参数 ci、截距和误差分别为回归系数、常数偏移量和误差。系数 ci 可解释为因变量(y 标签)随相应自变量(x 特征)的单位增加而增加。在下面的简单示例中,线性回归用于根据房屋面积(x 特征)估算房价(y 标签)。
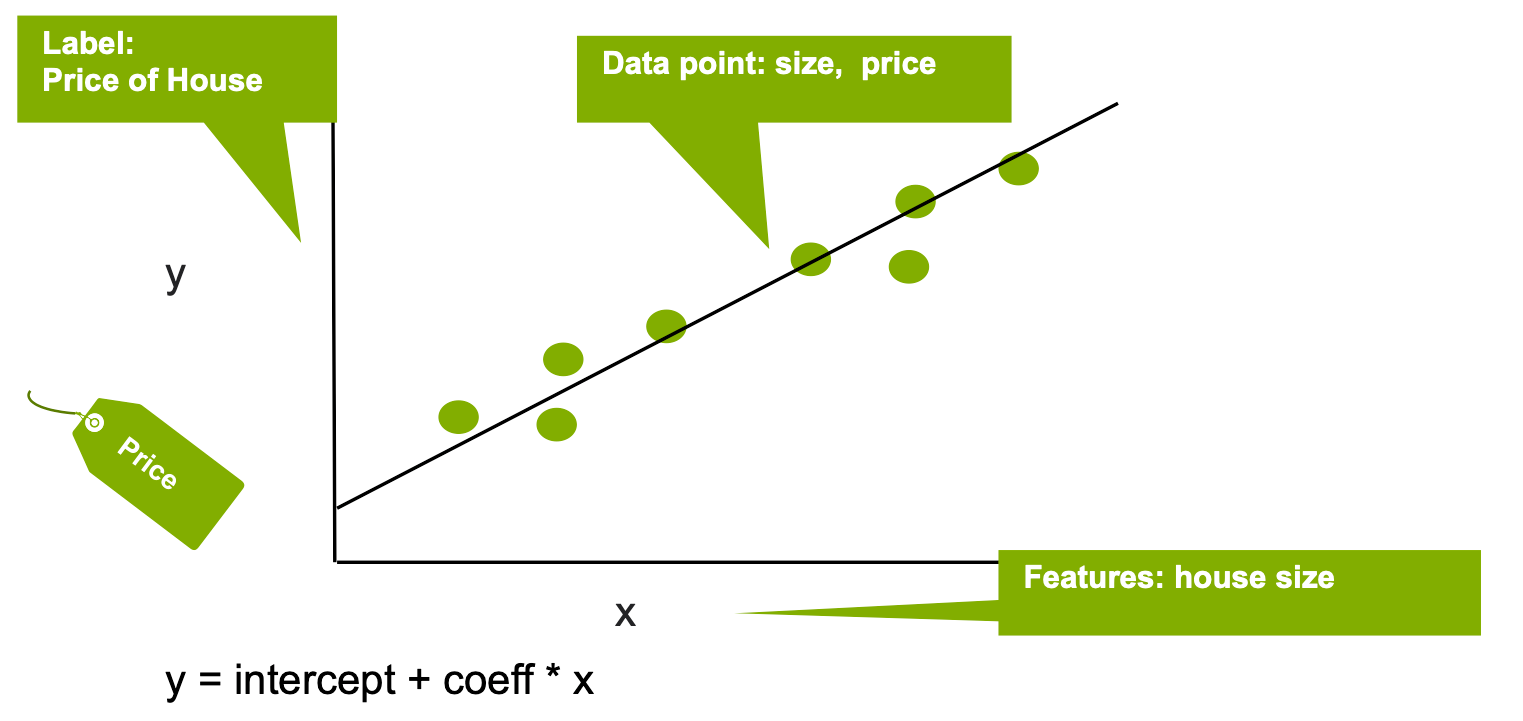
x 和 y 点与线之间的距离决定了自变量与因变量之间的连接强度。曲线斜率通常使用最小二乘法确定,该方法可尽可能降低曲线上点偏移量的平方的总和。
线性回归有两种基本类型 – 简单线性回归和多重线性回归。在简单线性回归中,一个自变量用于解释或预测一个因变量的结果。多重线性回归则使用两个或多个自变量来实现此目的。
回归通常用于预测结果。例如,回归可能是用于找出刷牙和蛀牙之间的关联。x 轴是给定群体中蛀牙的频率,而 y 轴是该群体中人刷牙的频率。每个人每周的刷牙频率及其蛀牙数量由图表上的一个点表示。在现实世界中,图表上将到处都是点,因为即使一些人经常刷牙也会出现蛀牙,而有些人即使不刷牙也不会出现蛀牙。但是,根据对蛀牙的已知信息,图表上所有点趋向的线可能会向下和向右倾斜。
回归分析的广泛应用之一是天气。当变量之间可建立强相关性时(例如大西洋东北部的海洋温度与飓风的发生率),我们可创建一个公式,根据自变量的变化预测未来事件。
回归分析还可用于金融场景,例如根据历史利率预测投资账户的未来价值。虽然每个月的利率各不相同,但从长远来看,出现了一些模式,可将其用于以合理的准确度预测增长和投资。
该技术还可用于确定关系不直观的因素之间的相关性。不过,需要牢记的是,相关性和因果关系是两个不同的因素。混淆它们可能会导致危险的误判。例如,冰激凌销量和溺水死亡的频率与第三因素(夏天)相关,但没有理由认为吃冰激凌与溺水有关。
此时,多重线性回归非常有用。它会检查多个自变量,以预测单个因变量的结果。它还假设因变量和自变量之间存在线性关系,残差(位于回归线上方或下方的点)属于法线,并且所有随机变量都有相同的有限方差。
多重线性回归可用于识别自变量影响的相对强度,并衡量任何一组自变量对因变量的影响。它比简单的线性回归更有用,因为问题集存在大量因素,例如预测商品价格。
第三种类型称为非线性回归,其中数据可拟合为模型,并可表示为数学函数。通常涉及多个变量,其关系会表示为曲线而非直线。非线性回归可估计自变量和因变量之间的任意关系模型。一个常见示例是随着时间的推移预测人口。虽然人口与时间之间有着密切的关系,但由于各种因素影响年年变化,因此这一关系并不是线性的。非线性人口增长模型可针对未实际测量的时间对人口做出预测。
什么是逻辑回归?
逻辑回归是一种分类模型,该模型使用输入变量(特征)来预测分类结果变量,而分类结果变量(标签)又可呈现出一组有限的分类值中的其中一个值。二项逻辑回归只限于两个二进制输出类别,而多项逻辑回归则可扩展至两个以上的输出类。逻辑回归示例包括将二进制条件分类为“健康”/“不健康”,或将图像分类为“自行车”/“火车”/“汽车”/“卡车”。
逻辑回归将逻辑 sigmoid 函数应用于加权输入值以生成数据类预测。
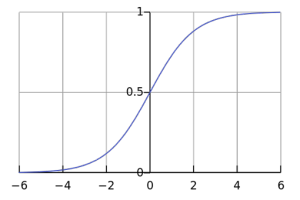
图:逻辑 sigmoid 函数 。图像来源
逻辑回归模型可预测作为自变量函数值的因变量的概率。因变量是我们尝试预测的输出(标签),而自变量或特征是我们认为可能影响输出的因素。
广义线性回归无需数据输入,也可具有正态分布。测试数据可具有任何分布。逻辑回归是广义线性回归的特例,其中响应变量须遵循 logit 函数。logit 函数的输入为概率 p,值介于 0 和 1 之间。概率 p 的比值比定义为 p/(1-p),logit 函数定义为比值比或对数几率的对数。
Logit(p) = Log(odds) = Log (p/(1-p))
逻辑回归模型的质量由拟合度量和预测能力决定。R 平方是一个衡量指标,可以根据因变量度量对逻辑函数中自变量的预测效果,取值范围介于 0 到 1 之间。计算 R 平方的方法有很多,包括 Cox-Snell R2 和 McFadden R2。另一方面,我们还可使用 Pearson 卡方、Hosmer-Lemeshow 和 Stukel 测试等测试方法来度量拟合优度。正确测试类型的选用标准取决于多个因素,诸如 p 值分布、相互作用和二次效应以及数据分组。
逻辑回归的应用
逻辑回归类似于非线性感知器或无隐藏层的神经网络。逻辑回归在数据稀缺领域具有极高的应用价值,例如在医学和社会科学领域中,逻辑回归可用于分析和解释实验结果。由于回归简单快速,因而也适用于十分庞大的数据集。不过,逻辑回归无法用于预测连续结果或与非独立数据集一并使用。使用逻辑回归时,还可能出现模型过拟合数据的情况。
为何选择回归?
机器学习模型的主要用途之一是预测结果。这也是回归分析的主要价值。回归是一种监督式学习技术,可帮助找到变量之间的相关性,并基于一个或多个预测变量预测连续输出。机器学习算法可以为此类功能使用不同类型的回归分析,例如根据过去的购买模式预测客户购买产品的可能性、根据物体的特性对物体进行分类,以及确定卡车路线变化对按期交付的影响。
使用最小二乘法模型计算回归线的斜率是一项非常耗时的任务,很适合机器学习。结果和回归模型的质量也随所考虑变量的数量而提升。机器学习算法可以考虑大量人为变量,从而在引入额外变量时产生更好的结果。